Spline Shapes
IPKISS has a number of classes for shapes built from splines. Splines are used in many graphical design and CAD tools. They are polynomial parametric functions that can be used to perform a smooth interpolation between a small set of control points.
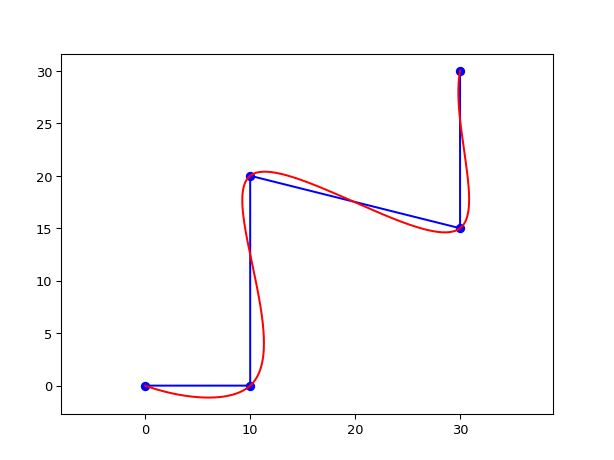
Shape fitting a natural spline through all points of the |
|
Shape fitting a spline through all points of the |
ShapeFitNaturalCubicSpline
- class ipkiss3.all.ShapeFitNaturalCubicSpline
Shape fitting a natural spline through all points of the
original_shape. The end points are ‘natural’, i.e. they have zero curvature. A third-order spline is used to guarantee continuity of tangent and curvature.The
start_face_angleandend_face_angleof theoriginal_shapeare not taken into account.When
original shapeis closed, the spline will also be closed, and continuous in curvature and tangent in the start/end point, rather than having zero curvature in those points.- Parameters:
- original_shape: Shape, required
- discretisation: float and number > 0, optional
default (approximate) distance between evaluated points. Default is 100 grid spaces
- end_face_angle: float, optional
- start_face_angle: float, optional
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
- closed: locked
Examples
from ipkiss3 import all as i3 from matplotlib import pyplot as plt s = i3.Shape([(0.0, 0.0), (10.0, 0.0), (10.0, 20.0), (30.0, 15.0), (30.0, 30.0)]) s2 = i3.ShapeFitNaturalCubicSpline(original_shape=s, discretisation=0.1) # plot control shape x, y = s.points.transpose() plt.plot(x, y, "bo-") # plot spline x2, y2 = s2.points.transpose() plt.plot(x2, y2, "r-") plt.axis("equal") plt.show()
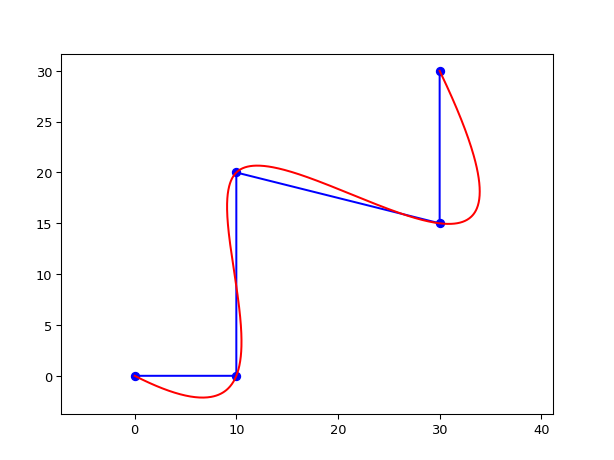
ShapeFitClampedCubicSpline
- class ipkiss3.all.ShapeFitClampedCubicSpline
Shape fitting a spline through all points of the
original_shape. A third-order spline is used to guarantee continuity in both tangent and curvature.The start and end angle are clamped to match the
start_face_angleandend_face_angleof the original shape, as well as zero curvature in those points.If the
original_shapeis closed, the spline will also be closed, but will still adhere to the clamped conditions (i.e. tangent and zero curvature) in the start/end point. Unless thestart_face_angleandend_face_angleare identical, the spline will not be smooth (continuous in tangent and curvature) in those points.- Parameters:
- original_shape: Shape, required
- discretisation: float and number > 0, optional
default (approximate) distance between evaluated points. Default is 100 grid spaces
- end_face_angle: float, optional
- start_face_angle: float, optional
- points: optional
points of this shape
- Other Parameters:
- size_info: SizeInfo, locked
get the size information on this Shape
- closed: locked
Examples
from ipkiss3 import all as i3 from matplotlib import pyplot as plt s = i3.Shape( [(0.0, 0.0), (10.0, 0.0), (10.0, 20.0), (30.0, 15.0), (30.0, 30.0)], start_face_angle=-20.0, end_face_angle=80.0, ) s2 = i3.ShapeFitClampedCubicSpline(original_shape=s, discretisation=0.1) # plot control shape x, y = s.points.transpose() plt.plot(x, y, "bo-") # plot spline x2, y2 = s2.points.transpose() plt.plot(x2, y2, "r-") plt.axis("equal") plt.show()