Scatter matrix: a mathematical primer
This is a short mathematical introduction into scatter matrices.
In a passive, linear circuit, we can treat an optical structure as a black box which exchanges energy with the outside world through several physical outlets. Figure An optical structure as a black box with several terms. shows how a structure has different physical outlets, which we will call optical terms (or terms, in short). These terms can be associated with an optical waveguide mode, or a free space electromagnetic beam.
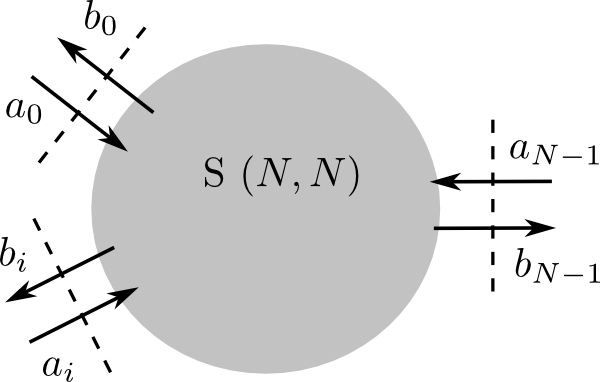
An optical structure as a black box with several terms.
We define \(a_i\) and \(b_i\) as the complex amplitude of the ingoing, resp. outgoing normalized electromagnetic mode. If the circuit is linear, we can define the following relationship between the outputs \(B \in (b_0, ...,b_{N-1})\) and the inputs \(A \in (a_0, ...,a{N-1})\):
Where we have defined the scatter matrix \(\mathbf{S}\) (NxN).
Note
In this description, the different modes are expanded into different terms. So, suppose a component has four physical terms, and there are two modes per term, the S-matrix has the following dimension: (8 x 8).
Attention
Due to the way the scatter matrix is defined, S[a, b] means: from port b to port a. For reciprocal devices (which is usually the case), S[a, b] = S[b, a], so it doesn’t matter in which direction you look at the transmission. But when working with Non-reciprocal devices, it is very important to be aware of this.
Properties of the scatter matrix
Depending on the actual material properties and geometry inside the structure, the component can have two interesting properties: passivity and reciprocity.
passivity: A component is told to be passive when it is unable to generate energy. This means that (we assume the \(\mathbf{S}\)-matrix is time-invariant), \(\left|| \mathbf{B} \right|| \leq \left|| \mathbf{A} \right||\). If we square both sides and use \(\left|| \mathbf{A} \right||^2 = \mathbf{A}^H \mathbf{A}\), we get:
\[\mathbf{A}^H \left( \mathbf{I} - \mathbf{S}^H \mathbf{S} \right) \mathbf{A} \geq \mathbf{0},\]for all possible values of \(\mathbf{A}\). This is equivalent to saying that the matrix \(\mathbf{I} - \mathbf{S}^H \mathbf{S}\) is semi-positive definite.
For a lossless component, the equality holds. In this case, this is equivalent to the condition that \(\mathbf{S}\) is an unitary matrix, i.e.,
\[\mathbf{S}^H \mathbf{S} = \mathbf{1},\]where \(\mathbf{S}^H\) is the conjugate transpose of \(\mathbf{S}\).
When the \(\mathbf{S}\)-matrix is varying through time, the conditions for being passive are more complicated. Apart from the condition that the component should absorb more energy than it generates, the possible generation should happen after absorption. For more details we refer to [triverio2007stability].
reciprocal: If a circuit is made of symmetrical constitutive parameters, i.e. the permittivity \(\epsilon=\epsilon^T\) and the permeability \(\mu=\mu^T\), then the circuit is called reciprocal. This is almost always the case, except for magnetic materials in the presence of a magnetic field. It can be proven that for a reciprocal component, \(\mathbf{S}\) is a symmetrical matrix, i.e.,
\[\mathbf{S} = \mathbf{S}^T,\]and hence the transmission between two ports does not depend on the propagation direction.
See also:
Non-reciprocal devices
Please note that, because of \(\mathbf{B} = \mathbf{S} \cdot \mathbf{A}\), the transmission \(S[a, b]\) means: from port \(b\) to port \(a\). This might seem confusing at first sight. The following image illustrates how the S-matrix of a simple optical isolator looks like:
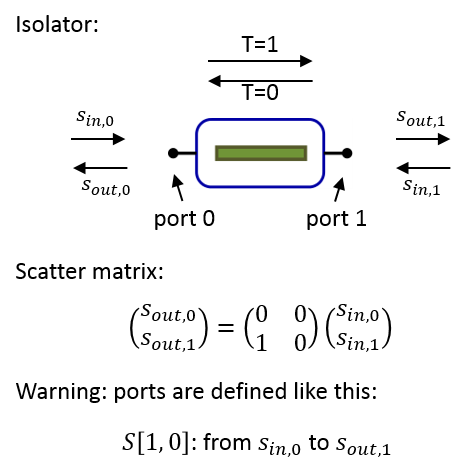
Example of a non-reciprocal component: an optical isolator.
Please keep this in mind when you define non-reciprocal devices.
See also:
Piero Triverio, Stefano Grivet-Talocia, Michel S Nakhla, Flavio G Canavero, and Ramachandra Achar. Stability, causality, and passivity in electrical interconnect models. Advanced Packaging, IEEE Transactions on, 30(4):795–808, 2007.